티스토리 뷰
혼동될 수 있는 도심(Centroid), 무게중심, 중립축(Neutral Axis)의 개념을 정리해보고 차이점을 파악해보았다.
도심 (Centroid)
도심(centroid)이란 어떤 임의 단면에서 직교 좌표축에 대한 단면 1차 모멘트가 0이 되는 점을 말한다. 직교 좌표축에서 도심까지의 거리를 구하는 방법은 단면 1차 모멘트를 도형의 면적으로 나누면 된다.


무게중심(Center of Gravity)
무게중심이란 중력에 의한 단면 1차모멘트(알짜 토크)가 0인 점이다. 즉 물체의 각 부분에 작용하는 중력의 합력의 작용점을 말한다. 물체의 종류에 관계없이 그 부분에 실을 매달았을 때, 물체가 균형을 이루는 내부의 한 점이라고 말할 수도 있다. 물체가 균일한 물질로 이루어져 있다면, 단면의 도심과 무게중심은 일치한다.

도심과 무게중심
도심은 전체 "면적"과 "면적"의 1차 모멘트
무게중심은 "면적"에 해당하는 무게, 즉 "중력"을 고려한 것이므로, 단면이 균일한 재료를 사용한 경우에는 두 값은 같다.


중립축 (Neutral Axis)
한 방향으로 굽힘이 발생하면 단면에 인장과 압축이 발생한다. 이 인장과 압축의 중간쯤에는 인장도 아니고 압축도 아닌 중립 지대가 있을 것인데 이 위치가 중립 면(neutral plane)이 이다. 즉, 보에 휨모멘트가 작용하였을 경우, 단면에 수직응력과 변형율이 0이되는 점을 연결한 직선이다.


보에 순수 휨이 작용할 경우, 단면 내 깊이에 따른 응력 분포는 아래와 같다.

이 때, 단면 내부에는 인장과 압축력의 힘의 평형이 이루어져야 한다.
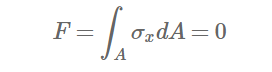

따라서, 균일한 재료로 이루어진 단면에서 중립축과 도심은 일치한다.

'구조 설계 및 시방서 > 재료구조역학' 카테고리의 다른 글
| 좌굴(Buckling)과 P-Delta 효과 (0) | 2023.04.04 |
|---|---|
| Plain Strain / Plain Stress (0) | 2021.05.22 |
| 뒤틀림(Distortion), 뒴(Warping) (0) | 2020.02.05 |
